<그래프(graph)>
선형 자료구조나 트리 자료구조로 표현하기 어려운 多:多의 관계를 가지는 원소들을 표현하기 위한 자료구조
그래프 G
- 객체를 나타내는 정점(vertex)과 객체를 연결하는 간선(edge)의 집합
G = (V, E)
- V는 그래프에 있는 정점들의 집합
- E는 정점을 연결하는 간선들의 집합
그래프사용 예 : 버스노선도, 지하철노선도, 인맥 지도, 길찾기, 최단거리 구하기
<그래프의 종류>
1. 무방향 그래프(undirected graph)
두 정점을 연결하는 간선의 방향이 없는 그래프이며, 정점 Vi와 정점 Vj을 연결하는 간선을 (Vi, Vj)로 표현 - (Vi, Vj)와 (Vj, Vi)는 같은 간선을 의미.
V(G1)={A, B, C, D} E(G1)={(A,B), (A,D), (B,C), (B,D), (C,D)}
V(G2)={A, B, C} E(G2)={(A,B), (A,C), (B,C)}
G1 G2
G3 G4
3. 완전 그래프(complete graph)
각 정점에서 다른 모든 정점을 연결하여 가능한 최대의 간선 수를 가진 그래프이다.
정점이 n개인 무방향 그래프에서 최대의 간선 수 : n(n-1)/2개
정점이 n개인 방향 그래프의 최대 간선 수 : n(n-1)개
완전 그래프의 예
- G5는 정점의 개수가 4개인 무방향 그래프이므로 완전 그래프가 되려면 4(4-1)/2=6개의 간선 연결
- G6은 정점의 개수가 4개인 방향 그래프이므로 완전 그래프가 되려면 4(4-1)=12개의 간선 연결
G5 G6
4. 부분 그래프(subgraph) : G'
원래의 그래프에서 일부의 정점이나 간선을 제외하여 만든 그래프이다.
그래프 G와 부분 그래프 G'의 관계
V(G')⊆V(G), E(G')⊆E(G)
그래프 G1에 대한 부분 그래프의 예
G1 G`
5. 가중 그래프(weight graph) , 네트워크(network)
정점을 연결하는 간선에 가중치(weight)를 할당한 그래프
G7 G8
<그래프 관련 용어>
1. 그래프에서 두 정점 Vi과 Vj를 연결하는 간선 (Vi, Vj)가 있을 때, 두 정점 Vi와 Vj를인접(adjacent)되어 있다고 하고,
2. 간선 (Vi, Vj)는 정점 Vi와 Vj에 부속(incident)되어있다고 한다.
ex) 그래프 G1에서 정점 A와 인접한 정점은 B와 D이고, 정점 A에 부속되어 있는 간선은 (A,B)와 (A,D)이다.
G1
G3
3. 차수(degree) – 정점에 부속되어있는 간선의 수
ex) 무방향 그래프 G1에서 정점 A의 차수는 2, 정점 B의 차수는 3
방향 그래프의 정점의 차수 = 진입차수 + 진출차수
- 방향 그래프의 진입차수(in-degree) : 정점을 머리로 하는 간선의 수
- 방향 그래프의 진출차수(out-degree) : 정점을 꼬리로 하는 간선의 수
- 방향 그래프 G3에서 정점 B의 진입차수는 1, 진출차수는 2
정점 B의 전체 차수는 (진입차수 + 진출차수) 이므로 3이 된다.
4. 경로(path) - 그래프에서 간선을 따라 갈 수 있는 길을 순서대로 나열한 것 즉, 정점 Vi에서 Vj까지 간선으로 연결된 정점을 순서대로 나열한 리스트
ex) 그래프 G1에서 정점 A에서 정점 C까지의 경로 : A-B-C 경로, A-B-D-C 경로, A-D-C 경로, A-D-B-C 경로
5. 경로길이(path length) - 경로를 구성하는 간선의 수
6. 단순경로(simple path) - 모두 다른 정점으로 구성된 경로
ex) 그래프 G1에서 정점 A에서 정점 C까지의 경로 A-B-C는 단순경로이고, 경로 A-B-D-A-B-C는 단순경로가 아니다.
7. 사이클(cycle) - 단순경로 중에서 경로의 시작 정점과 마지막 정점이 같은 경로
ex) 그래프 G1에서 단순경로 A-B-C-D-A는 사이클이 된다.
8. DAG(directed acyclic graph) - 방향 그래프이면서 사이클이 없는 그래프
9. 연결 그래프(connected graph) - 서로 다른 모든 쌍의 정점들 사이에 경로가 있는 그래프 즉, 떨어져있는 정점이 없는 그래프
그래프에서 두 정점 Vi에서 Vj까지의 경로가 있으면 정점 Vi와 Vj가 연결(connected)되었다고 한다.
10. 트리는 사이클이 없는 연결 그래프이다.
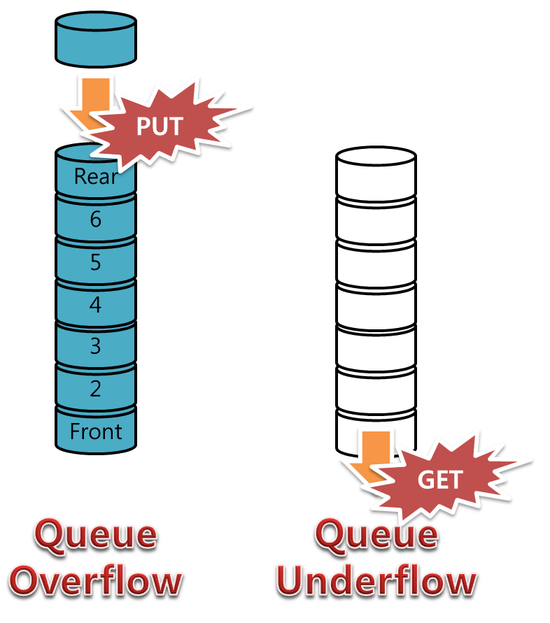
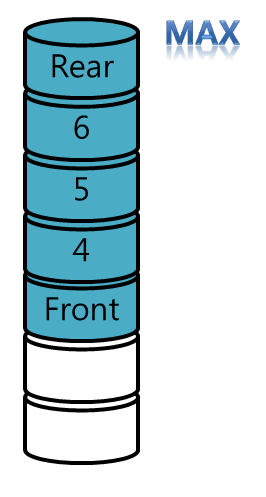
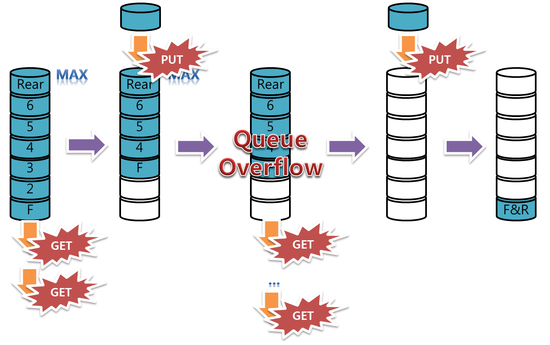
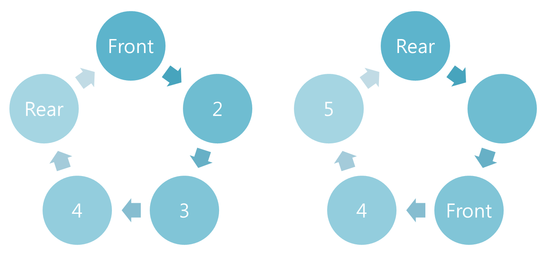
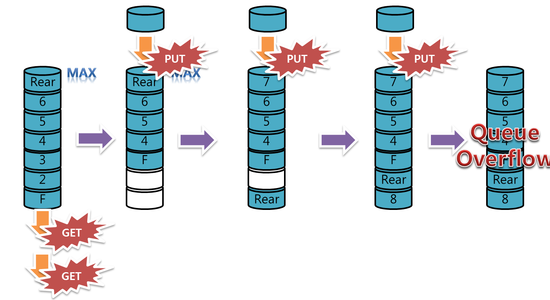
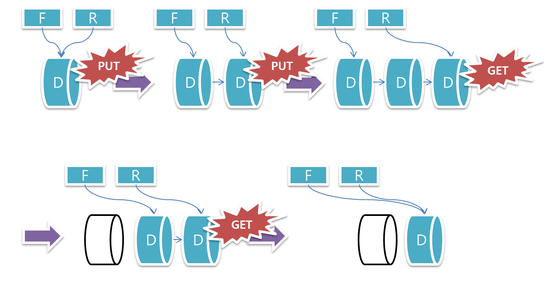
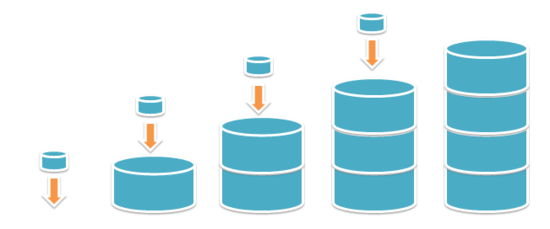
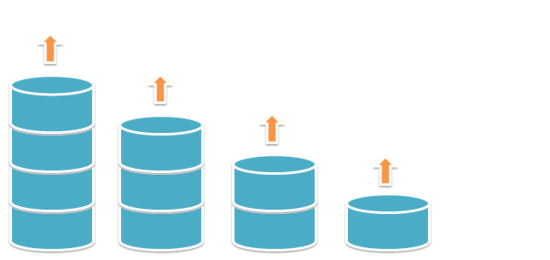
'Computer Engineering > Data Structure' 카테고리의 다른 글
| [자료구조] 트리(Tree) (0) | 2016.02.04 |
|---|---|
| [자료구조] 연결리스트(Linked List) (0) | 2016.02.04 |
| [자료구조] 큐(Queue) (0) | 2016.02.04 |
| [자료구조] 스택(Stack) (0) | 2016.02.03 |
| [자료구조] 개념과 종류 (0) | 2016.02.03 |